|
|
 日程： ２０１６年１月２１日（木）10:00 〜 16:15
| ||||||||||||
|
場所： 東京大学大学院数理科学研究科棟 128教室
| ||||||||||||
講師（講演順，敬称略）：
| ||||||||||||
 プログラム：
|
1．Danielle Hilhorst 氏： "Mathematical analysis of a three component chemotactic system"
Abstract：
We consider an initial-boundary value problem describing the formation of colony patterns of bacteria Escherichia coli.
This model consists of reaction-diffusion equations coupled with the Keller-Segel system from the chemotaxis theory in the space-time domain Ω×(0,∞),
where Ω is a bounded domain of $R^d$ with a sufficiently smooth boundary ∂Ω.
More precisely, we study the problem
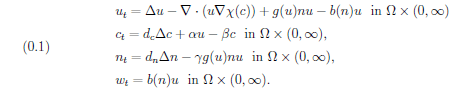
We supplement these equations with the Neumann boundary conditions
as well as with nonnegative initial data
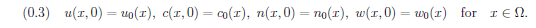
Here $u(x,t)$ denotes the density of active bacteria, $w(x,t)$ the density of inactive bacteria,
$n(x,t)$ the density of nutrient and $c(x,t)$ the concentration of chemoattractant. We remark
that the first three equations are closed for $u$, $c$ and $n$ and that if these are solved, then
$w$ can be obtained from $u$ and $n$.
We answer questions about the global in time existence of solutions as well as on their large time behavior.
Moreover, we show that the solutions of a related model may blow up in finite time.
This is joint work with Rafa l Celiński, Grzegorz Karch and Masayasu Mimura.
アブストラクトPDF版： Hilhorst
2．Thanh Nam Nguyen 氏： "Large time behavior, Lyapunov functionals and the rearrangement theory for a nonlocal differential equation: the periodically heterogeneous framework"
Abstract：
We consider an initial-boundary value problem for a nonlocal evolution equation of bistable type
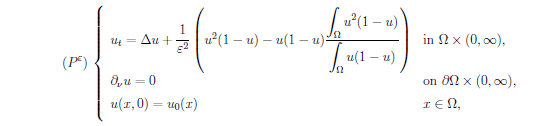
and study possible sharp transition layers at the very early stage that the solution of Problem $(P^ε)$ might develop as the parameter ε tends to zero.
Here Ω is a bounded domain of $\R^N (N≥1)$ with smooth boundary ∂Ω, and $∂_\nu$ is the outer normal derivative to ∂Ω.
It turns out that such transition layers can be investigated via the structure of the ω-limit set of the corresponding nonlocal ordinary differential equation.
We prove that for a large class of initial functions, the ω-limit set of the nonlocal ordinary differential equation only contains one element.
Furthermore, that element is a step function taking at most two values.
The proof bases on the rearrangement theory and the existence of infinitely many Lyapunov functionals.
This is a joint work with Danielle Hilhorst and Philippe Laurençot.
アブストラクトPDF版： Nguyen
3．Yasuhito Miyamoto 氏： "Classification of bifurcation diagrams for supercritical elliptic Dirichlet problems in a ball"
Abstract：
Let $B⊂\R^N$, N≥3, be a unit ball.
We study the shape of the bifurcation curve of the positive solutions to the supercritical elliptic equation in $B$
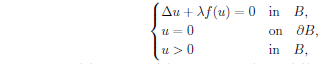
where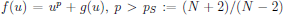 
and $g(u)$ is a lower order term.
This problem has a singular solution $(\lambda^*,u^*)$.
In this talk we classify the bifurcation curves with the number of the turning points $T$.
The Joseph-Lundgren exponent
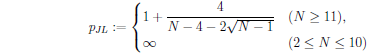
plays an important role.
We prove the following:
Let $m(u^*)$ denote the Morse index of $u^*$.
If $p_S<p<p_{JL}$, then $m(u^*)=∞$ and T=∞.
If $p≥p_{JL}$, then $m(u^*)<∞$.
In this case, if $m(u^*)=0$, then T=0, and hence a classical positive solution is unique when it exists.
If $m(u^*)≥1$, then $m(u^*)≤T<∞$.
In particular if N≥11, $p≥p_{JL}$, $m(u^*)≥1$, and $u^*$ is nondegenerate, then the last case occurs.
A typical example is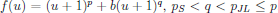 
.
Main tools are the intersection number, a singular Sturm-Liouville theory, and a phase plane analysis.
The talk is based on a joint work with Yuki Naito of Ehime University.
アブストラクトPDF版： Miyamoto
4．Thomas Giletti 氏： "Various effects of oscillations in reaction-diffusion equations"
Abstract：
A celebrated result of Aronson and Weinberger states that solutions of the reaction-diffusion equation
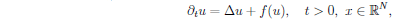
typically spread with a given speed $c^*$. More precisely, for typical choices of the nonlinearity~$f$, and for any compactly supported initial datum, the solution satisfies that
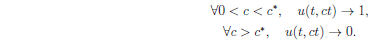
Moreover, we emphasize that the speed $c^*$ does not depend on the choice of any such initial datum.
In this talk, I will discuss how sensitive this result is to its assumptions, and more specifically to the introduction of some oscillations in various parameters.
In a first part, we will consider a KPP type equation with some spatial heterogeneity. Namely, the reaction $f(x,u)$ depends on the spatial variable and satisfies
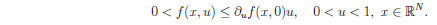
We will provide several examples inspired from the periodic case where the asymptotic speed may or may not vary throughout the propagation.
These examples will highlight the difficulty of characterizing the occurrence of spreading with constant speed.
In a second part, we look at an ignition type reaction-diffusion equation, i.e.
Due to the fact that reaction does not occur below the ignition threshold θ, it is natural to expect some spatial propagation even when the initial datum does not decay at infinity.
After presenting some results from the literature, we will describe how the speed depends non trivially on oscillations of the initial datum above the ignition threshold.
While this talk will be focused on examples (issued from several collaborations with Jimmy Garnier, François Hamel and Grégoire Nadin),
we will raise some new questions and try to provide a better understanding of the dynamics of reaction-diffusions equations in a general framework.
アブストラクトPDF版： Giletti
世話人： 俣野博， Danielle Hilhorst 問い合わせ先： matano
ms.u-tokyo.ac.jp
会場へのアクセスは，
http://www.ms.u-tokyo.ac.jp/access/index.html
にてご確認ください．